| Lo spazio |
|
Nella nostra esperienza quotidiana sugli oggetti che ci circondano siamo portati a definire delle relazioni di dimensioni e distanze quali ad esempio la lunghezza di un segmento, l'area di una superficie, il volume racchiuso da una superficie, la distanza tra due punti, l'angolo piano, la direzione di una retta , ecc.
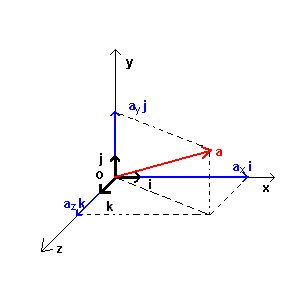Normalmente si identifica un punto nello spazio rispetto ad un osservatore ed il modo più comodo per farlo è considerare l'osservatore posto nell'intersezione degli assi cartesiani:
La posizione del punto P può essere descritta completamente , con riferimento ad O, dando le tre distanze di P nei rispettivi piani xy, xz, yz. In fisica le osservabili le possiamo distinguere in scalari e vettoriali: quelle scalari sono definite da una misura, come ad esempio la distanza tra due punti; quelle vettoriali altre ad avere una misura sono anche associate ad una direzione ed ad un verso come ad esempio la velocità in cui per definirla occorre darne il valore numerico la direzione ed il verso con cui si percorre la direzione data. Le operazioni tra grandezze scalari sono semplici in quanto sono le operazioni possibili con i numeri, quelle tra grandezze vettoriali devono tener conto anche della direzione e del verso. Riportiamo gli esempi delle principali operazioni vettoriali:
La differenza di due vettori a - b è uguale al vettore c che si ottiene dalla somma di a con l'opposto di b 
Un altro concetto importantissimo per comprendere i fenomeni fisici è quello del tempo infatti nell'osservare gli oggetti nello spazio ci accorgiamo dei loro mutamenti e per poter descrivere con un certo ordine questa proprietà del mutare degli oggetti usiamo l'unità di misura del tempo. In questo modo, per esempio, possiamo dire se due eventi sono avvenuti nello stesso momento. L'unità di misura del tempo è una durata campione che si può ottenere da fenomeni che si ripetono con regolarità e ottenere con sperimentazioni il numero di volte che la durata campione è contenuta in quella misura. L'unità di tempo è definita dai moti di rotazione e rivoluzione della Terra: l'anno solare è la durata di una rivoluzione della Terra intorno al Sole èd è come tutti sappiamo una unità di durata fondamentale. Si dice giorno solare il temo che intercorre fra due passaggi del Sole ad un meridiano luogo di osservazione; poiché sappiamo che la Terra ruota attorno al Sole con un'orbita ellittica il giorno solare non è costante ma varia un poco per cui si considera normalmente il giorno solare medio che vale 1/365,242 dell'anno solare. Normalmente si usano dei sottomultipli del giorno solare medio come:
Nello studio della meccanica è assolutamente fondamentale descrivere, per un evento che stiamo studiando, la sua posizione nello spazio e nel tempo. Nel sistema di riferimento spaziale (spazio Euclideo) possiamo, rispetto ad un osservatore posto nell'origine degli assi punto O, individuare ogni punto con le coordinate x,y,z dell'evento che stiamo esaminando; parallelamente il tempo può essere misurato ponendo un misuratore di tempo, esempio un orologio, in ogni punto e leggendo il valore del tempo nel momento in cui avviene l'evento con l'accortezza di aver sincronizzato tutti gli orologi sulla medesima scale di tempi. Per illustrare quanto descritto pensiamo ad un treno che parte da una stazione tempo uguale a ore 10,00 e che passa per due stazioni prima di arrivare alla stazione di destinazione, se in ogni stazione mettiamo un osservatore che misura, con orologi ovviamente sincronizzati, il valore del tempo al passaggio del treno possiamo con le osservazioni fatte descrivere il movimento del treno: il treno è partito alle ore 10,00 dalla stazione A, è passato alle ore 11,30 dalla stazione A(1) distante 50 chilometri dalla stazione A, è passato dalla stazione A(2), distante 70 chilometri dalla stazione A, alle ore 12,05, è arrivato alla stazione B, distante 120 chilometri dalla stazione A, alle ore 13,10. Con questo sistema è possibile, ad esempio. Misurare direttamente la velocità di propagazione della luce con il metodo di Fizeau o di Foucault: si fa partire da un punto A un segnale luminoso e lo si fa riflettere da un uno specchio posto in un punto B in modo tale che una parte del segnale ritorni in A e si misura il tempo che intercorre tra la partenza ed il ritorno in A del segnale luminoso, conoscendo la distanza tra il punto A e quello B possiamo calcolare il valore della velocità c come rapporto tra 2AB/T dove AB è la distanza tra il punti A e B e T è il tempo impiegato dal segnale luminoso per andare da A a B e tornare in A. Il risultato che si ottiene è c = 2,97 10 metri/secondo. In generale quando un corpo interagisce con altri si possono avere diversi effetti ad esempio il fatto che un corpo si mette in moto o cambia la sua velocità, che si deforma in modo elastico e permanente, o che non si osservano effetti come per una bilancia a piatti in equilibrio sulla quale si pongono pesi uguali, in questo caso la bilancia non si muove e non si deforma. In fisica si cerca di rappresentare le interazioni fra corpi con l'osservabile fisica definita "forza" che ci consente di dire che tra i corpi si esercitano delle forze, e che le variazioni di velocità o le deformazioni dei corpi sono dovute all'azione di queste forze. Le forze possono essere causa di un moto e allora consideriamo gli aspetti dinamici del corpo oppure possono non sortire effetti, perché le forze che agiscono sul corpo si fanno equilibrio, ed allora parliamo di aspetti statici. Diamo una sintetica descrizione di alcuni tipi di interazioni che si possono avere tra corpi:
Possiamo pertanto dire che se due forze F1 e F2 producono la stessa accelerazione su un corpo C allora le due forze hanno la medesima intensità, se la forza F1 fosse di intensità doppia della forza F2 allora l'accelerazione prodotta da F1 sul corpo C sarebbe doppia di quella prodotta dalla forza F2. Con questo ragionamento siamo in grado di confrontare delle forze tra di loro costruendo una scala di forze riferite all'oggetto C ( Traiettoria parabolica dei proietti ) . Possiamo sintetizzare dicendo che in generale le forze sono rappresentabili con dei vettori che hanno la direzione ed il verso dell'accelerazione che producono e l'intensità (modulo) proporzionale a quello dell'accelerazione. Abbiamo detto che è possibile costruire, in riferimento ad un corpo C, una scala di forze confrontabili ora vediamo cosa succede se applichiamo la stessa forza F su degli oggetti C , ad esempio dei cubi, costituiti da diversi materiali, ferro, legno, rame, ecc. Nell'ipotesi che non ci siano attriti i corpi C soggetti alla forza F si muoveranno con moto uniformemente accelerato e vedendo l'accelerazione prodotta possiamo dedurne quanto segue:
Possiamo pertanto dire che due corpi qualsiasi hanno la stessa massa quando soggetti alla stessa forza acquistano la stessa accelerazione. Praticamente questo significa che se su due corpi, C1 e C2, facciamo agire la stessa forza F e verifichiamo che le accelerazioni prodotte sono rispettivamente a1 sul corpo C1 e il doppio di a1 sul corpo C2 allora la massa di C1 è il doppio di quella di C2. Generalizzando possiamo dire che la massa di un corpo è un'osservabile fisica il cui valore è inversamente proporzionale al valore (modulo) dell'accelerazione: m proporzionale 1/a Possiamo anche dire che la massa di un corpo è direttamente proporzionale al suo volume: m proporzionale a V Per come abbiamo definito la massa di un corpo possiamo dire che essa rappresenta la proprietà dei corpi ad opporsi al moto per questo viene chiamata anche massa inerziale. Per misurare la massa si è scelto come unità di misura la massa di un decimetro cubo di acqua distillata a 4° centigradi, questa massa vale 1 Kgm . Possiamo concludere il ragionamento sulla forza dicendo che:
Abbiamo visto che quando una forza viene applicata ad un oggetto questa agisce sull'oggetto producendo dei cambiamenti visibili ad esempio quando solleviamo le sei bottiglie di acqua minerale dal piano stradale per portarle nel nostro appartamento posto al secondo piano di una casa senza ascensore; nel fare questa attività diciamo che stiamo compiendo un lavoro. E' evidente che se dobbiamo portare le bottiglie d'acqua al quarto piano compiamo un lavoro maggiore come è anche evidente che il lavoro è maggiore se le bottiglie diventano 12. Nel primo, cioè il passaggio dal secondo piano al quarto, fa cambiare lo spostamento che facciamo fare alle bottiglie, mentre nel secondo casa cambiamo il numero di bottiglie quindi la forza che applichiamo ad esse per spostarle. Da questa considerazione possiamo dedurre che il lavoro è una grandezza fisica proporzionale sia alla forza che applichiamo all'oggetto sia allo spostamento che ad esso facciamo fare. La forza e lo spostamento sono due osservabili fisiche definibili con dei vettori ovvero con delle grandezze definite da un valore numerico (modulo) una direzione e da un verso, mentre il lavoro è un'osservabile fisica scalare identificata da un valore numerico; il modo per correlare due vettori ad un valore scalare è quello, come abbiamo visto sopra nelle definizioni dei vettori, al loro prodotto scalare ovvero : Lavoro = Forza * Spostamento * coseno FS dove FS è l'angolo formato delle direzioni dei due vettori Forza e Spostamento. Il Lavoro viene espresso in Joule ed esprime il lavoro fatto dalla forza di un Newton per spostarsi di un metro: 1 joule = 1 newton * 1 metro Se dovessimo alzare di un metro un peso di 1 Kgm dovremmo sviluppare il lavoro di 9,8 joule; infatti la forza necessaria per sollevare un peso di 1 chilogrammo massa (Kgm) è data dalla relazione F = m * g dove g è l'accelerazione di gravità (g = 9,8 m/secondo * secondo) ed m la massa del mostro corpo pertanto F = 1 * 9,8 uguale a 9,8 Newton (N) da cui L = 9,8 *1 uguale a 9,8 joule, se la massa da sollevare, sempre di un metro, fosse di 10 Kgm il lavoro da compiere sarebbe di 98 joule. Nelle considerazioni fin qui fatte l'osservabile tempo non è stata presa in considerazione però ci rendiamo tutti conto che se dovessimo spostare i 10 Kgm di un metro in 10 secondi o in 1 secondo la differenza esiste, la relazione che lega il lavoro fatto per il tempo impiegato a farlo si chiama potenza che si definisce come il lavoro svolto nell'unità di tempo e si indica con la relazione: P (potenza) = Lavoro / tempo La potenza si esprime in joule / secondo e questa relazione prende il nome di watt. Per fare qualche esempio se volessimo calcolare qual è il lavoro necessario per sollevare dal piano terra al secondo pianole 6 bottiglie di una confezione di acqua minerale e qual è la potenza spesa sapendo che si impiegano 30 secondi per arrivare dal piano terra al secondo piano con le bottiglie ovviamente in una condizione di assenza di attrito ( realmente non sarebbe possibile), dovremmo sapere: a) quanto pesiamo noi, ad esempio 70 kgm, b) quanto pesa la confezione di 6 bottiglie d'acqua ( 6 bottiglie da 1,5 litri d'acqua per bottiglia, ogni litro d'acqua pesa 1kgm pertanto il risultato è di 9 Kgm), c) quanti metri dista il secondo piano dal piano terra ad esempio 8 metri. Il calcolo si sviluppa nel modo seguente: per portare le bottiglie dal piano terra al secondo piano dobbiamo sollevare noi stessi più le bottiglie e per questo occorre una forza almeno uguale al peso nostro più quello delle bottiglie: F = m * g F = (70 + 9) * 9,8 = 774,2 N (Newton) Il lavoro speso é dato dalla relazione: L = F * S * cos(FS) dove s è lo spostamento verticale che vale 8 metri mentre FS è l'angolo tra la direzione della forza e lo spostamento e vale 0° in quanto la direzione della forza è verticale come la direzione dello spostamento, questo implica che il cos(FS) = 1 L = 774,2 * 8 *1 = 6193,6 J (joule) La potenza consumata per portare in 30 secondi le 6 bottiglie dal piano terra al secondo piano è data dalla relazione : P = L/t P = 6193,6 / 30 = 206,45 W (watt) Abbiamo definito che l'energia è l'attitudine dei corpi o dei sistemi a compiere lavoro, come abbiamo visto essa assume molte forme che sono correlate alle caratteristiche dei corpi e alle loro interazioni con l'ambiente. Il legame esistente tra il lavoro e l'energia consiste nel fatto che il lavoro fatto in un processo è uguale all'energia utilizzata per compiere tale processo. Possiamo pertanto dire che il lavoro rappresenta il processo attraverso il quale l'energia si scambia o si trasforma in un'altra. Poniamoci ora il problema di quanto lavoro si deve compiere per sollevare verticalmente un grave C di massa m uguale ad 10 Kgm, posto sul pavimento della nostra stanza, fino sul piano del tavolo in cucina. Questo spostamento lo facciamo una prima volta direttamente dal pavimento al piano del tavolo ed una seconda volta in due tempi: prima dal pavimento al piano della sedia, poi dalla sedia al piano del tavolo. Si ricorda che la seduta di una sedia è 45 centimetri da terra, il piano di un tavolo è a 70 centimetri da terra. Il corpo è soggetto alla forza di gravità quindi il suo peso, che ricordiamo è rappresento da una forza diretta verticalmente verso il basso (centro della Terra) è uguale a: P = m * g P = 10 * 9,8 P = 98 Newton (N) Per sollevare il corpo di peso P è necessario applicargli una forza F uguale e contraria ovvero diretta verso l'alto e del valore di 98 Newton (N). Nel primo caso che abbiamo, ovvero lo spostare direttamente il grave C dal pavimento al piano del tavolo è necessario compiere un lavoro pari a: L = F * s cos Fs poiché la direzione della forza F e dello spostamento sono uguali il loro angolo è di 0° quindi il coseno vale 1 L = 98 * 0,7 * 1 L = 68,6 joule (j) Nel secondo caso solleviamo il corpo C prima fino alla sedia posta a 0,45 metri dal pavimento compiendo un lavoro pari a: L1 = 98 * 0,45 * 1 L = 44,1 joule (j) Successivamente solleviamo il corpo C dalla seduta della sedia al pian del tavolo, in questo caso il nostro piano di riferimento è quello della sedia per cui lo spostamento che facciamo compiere al grave vale 25 centimetri (0,25 metri) di conseguenza il lavoro da compiere vale : L2 = 98 * 0,25 * 1 L = 24,5 joule (j) In questo caso il lavoro totale speso per sollevare il corpo C dal pavimento al piano del tavolo è la somma dei due lavori spesi: Ltot = L1 + L2 Ltot = 44,1 + 24,5 Ltot = 68,6 joule (j) In entrambi i casi il lavoro speso per sollevare il corpo C di peso uguale a 98 Newton dal pavimento al piano del tavolo è identico e vale 68,6 joule. La domanda che dobbiamo porci è la seguente: dove è finito tutto il lavoro che abbiamo speso per sollevare il corpo C ? La risposta è la seguente: il lavoro speso misura l'energia trasferita al corpo dalla forza che abbiamo utilizzato per sollevarlo al piano del tavolo e che ritroviamo come energia legata alla posizione del corpo ovvero alla sua altezza rispetto al piano di riferimento che abbiamo utilizzato: questa energia prende il nome di Energia Potenziale Gravitazionale, potenziale perché rimane tale finché in qualche modo non la sei espliciti, gravitazionale perché è dovuta alla presenza della forza di gravità Dal concetto di lavoro passiamo a uno dei più importanti concetti della fisica: il concetto di energia. La sua importanza è dovuta al fatto che qualunque fenomeno (fisico, chimico, biologico o che riguardi un qualsiasi aspetto dell'attività umana), può essere analizzato in termini di trasferimento o di trasformazione di energia e come abbiamo detto l'energia è un «qualcosa» che permette di compiere un lavoro. Nel linguaggio comune la parola «lavoro» è usata nelle circostanze più diverse ed esempio il lavoro compiuto rispettivamente da un uomo, da un animale, da una macchina. Un corpo in movimento possiede un'energia chiamata cinetica. Essa è tanto maggiore quanto più grandi sono la velocità del corpo e la sua massa. Ipotizziamo un corpo di massa m fermo sottoposto a una forza F costante per un certo tempo t. Il moto del corpo è accelerato, con accelerazione a = F/m, e dopo il tempo t il corpo avrà percorso lo spazio s definito dalla relazione s = 1/2 a * t2. La velocità, che il corpo avrà acquistato dopo il tempo t sarà data dalla relazione v = a * t. Il lavoro compiuto dalla forza F sul corpo è L = F * s, poiché F = a * m, possiamo anche scrivere L = a * m * s, sostituendo ad s il suo valore calcolato da s = 1/2 a * t2 avremo L = a * m * 1/2 a * t2 ovvero L =1/2 * m * a2 * t2, poiché la velocità v = a * t e v2 = a2 * t2 sostituendo avremo: L = 1/2 m v2 Per interpretare questo risultato ricordiamo che il lavoro compiuto misura la quantità di energia che si è dovuta spendere per far muovere il corpo ma, allo stesso tempo, misura la quantità di energia che il corpo ha acquistato e che equivale a 1/2* m * v2. Il risultato è quindi il seguente: un corpo di massa m e velocità v possiede un'energia cinetica Ec = 1/2 m * v2 L'energia cinetica, come del resto qualunque forma di energia, ha la stessa unità di misura del lavoro: se m è misurata in chilogrammi-massa e v in metri al secondo, l'energia cinetica è misurata in joule. ENERGIA POTENZIALE Consideriamo adesso un corpo di massa m che si trovi a un'altezza h dal suolo se lo facciamo cadere esso è capace di fare una buca nel terreno, oppure, se collegato a una carrucola, è in grado di sollevare un altro peso più leggero. Questo tipo di energia si chiama energia potenziale gravitazionale, ed è dovuta all'attrazione terrestre, essa è chiamata più semplicemente energia potenziale. Tanto più alte sono l'altezza h o quanto più grande è la massa m, maggiore è l'energia potenziale posseduta dal corpo. Definiamo ora l'espressione che esprimere l'energia potenziale. Ipotizziamo che il corpo sia collocato inizialmente al suolo, per alzarlo bisogna applicare ad esso una forza F appena superiore ai suo peso P, che è dato dal prodotto della massa m del corpo per l'accelerazione di gravità g, ovvero P = m * g , ne consegue che per alzare il corpo a un'altezza h si deve compiere un lavoro dato da: L = F * s = m * g * h Questo lavoro, compiuto a spese della nostra energia muscolare, valorizza quanta energia è stata acquistata dal corpo, cioè quanta energia esso possiede quando si trova all'altezza h definita come energia potenziale. L'energia potenziale di un corpo di massa m che si trovi a un'altezza h dal suolo è Ep = m * g * h Misurando m in chilogrammi-massa, h in metri e ponendo g = 9,8 m/s2, l'energia potenziale è di nuovo misurata in joule. Osserviamo cosa succede nel caso di un corpo in caduta, essendo il corpo sceso del tratto s, si trova ora all'altezza ha, la forza-peso P = m * g ,che agisce sul corpo, ha compiuto il lavoro L = P*s = m*g*s. Il lavoro speso per far scendere il corpo ha fatto diminuire la suaenergia potenziale infatti prima era Ep = m * g * h e poi è divenuta Ep = m * g * ha, quindi: Ep (iniziale) - Ep, (finale) = m * g * h - m * g * ha = m * g. * s. Contemporaneamente però è aumentata l'energia cinetica del corpo, che cadendo, e ha aumentato la sua velocità. Lo spostamento s è dato dalla relazione anche dalla relazione s = 1/2 g * t2 per cui il lavoro L = m*g*s può essere espresso come L = m*g*1/2 g * t2 = 1/2 *m2 * g2 * t2 ma la velocità del acquistata dal corpo è uguale all'accelerazione di gravità g moltiplicata per la sua massa m quindi v2 = g2 * t2 ne consegue che il lavoro è L = 1/2 *m2 * v2 Possiamo concludere quindi che, cadendo del tratto s, il corpo ha perso tanta energia potenziale quanta ne ha acquistata sotto forma d'energia cinetica. Se il corpo continua a cadere, l'energia potenziale diminuisce ancora ma sempre della stessa esatta quantità di cui aumenta l'energia cinetica. Viceversa, se un corpo viene lanciato verso l'alto la sua energia cinetica diminuisce perché la velocità diventa sempre minore, mentre l'energia potenziale aumenta esattamente della stessa quantità. Quanto abbiamo detto dimostra che, se durante il moto di un corpo consideriamo la somma della sua energia cinetica con quella potenziale, tale somma avrà sempre lo stesso valore, poiché di tanto aumenta o diminuisce la prima, e di tanto diminuisce o aumenta la seconda essa è E = Ep+ Ec Tale somma rappresenta l'energia totale del corpo, che si può manifestare nelle due forme d'energia potenziale o cinetica e che durante il moto si ha una continua trasformazione dell'una nell'altra senza però che l'energia totale cambi. Il principio di conservazione dell'energia è uno dei principi più importanti universali della fisica. Noi ne abbiamo considerato solo un caso molto semplice e particolare, ma si può estendere a un numero grandissimo di fenomeni che implicano varie forme di energia: tale principio afferma che in ogni processo fisico vi può essere trasformazione da una forma di energia a un'altra o trasferimento di energia da un corpo a un altro, ma l'energia complessiva di tutto il sistema di corpi considerato rimane sempre rigorosamente la stessa. |
|||||||||||||||||||||||||||||||||||||||||
 Torna a "Energia cinetica ed energia potenziale" |
| Che cos'è l'energia I Breve storia dell'energia I Fonti di energia I Impatto ambientale I Che fare I Link e credits |
| Credits |  |
Mappa del sito |